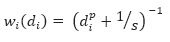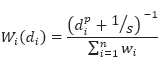3D Inverse Distance Weighted Gridding

Use the Voxel > New > Inverse Distance Weighted Gridding menu option (geogxnet.dll(Geosoft.GX.VoxUtils.VoxelIDWGridding;Run)*), to create a voxel file from a data channel in a database.

3D Inverse Distance Weighted Gridding dialog options

Channel to grid	Select a channel to grid from the list. Current X, Y and Z channels are required. The data channel may be an array channel, as long as the Z channel is also an array channel with the same number of columns, with the individual values in the Z channel columns corresponding to the individual data values in the data channel columns. Script Parameter: 3D_IDW_GRIDDING.CHANNEL
Output voxel name	Choose a file name for the output voxel. Script Parameter: 3D_IDW_GRIDDING.VOXEL
Cell size	Choose a horizontal (X and Y) cell size for the output voxel. The calculate button determines a default cell size which will give approximately one thousand voxel point locations, after calculating the bounding volume of the data, and assuming the vertical (Z) cell size is the same as the horizontal cell size. Script Parameter: 3D_IDW_GRIDDING.CELL_SIZE
Cell size for Z	By default, the vertical cell size is chosen to be the same as the horizontal cell size. Script Parameter: 3D_IDW_GRIDDING.CELLSIZEZ
Weighting power	This parameter modifies the shape of the weighting function. See “The Inverse-Distance Weighting Function: Defining the Weighting Slope and Power” below. Specify a value greater than or equal to zero. Script Parameter: 3D_IDW_GRIDDING.WEIGHT_POWER (Default: 2)
Weighting slope	This parameter modifies the steepness of the inverse distance-weighting function. See “The Inverse-Distance Weighting Function: Defining the Weighting Slope and Power” below. Script Parameter: 3D_IDW_GRIDDING.WEIGHT_SLOPE (Default: 1)
Search radius	For each voxel cell centre point, all values within the search radius are included in the weighted average, yielding the value at that point. The default is determined based on the number of cells in X and Y, and is at least 4 times the horizontal cell size. If no value is entered, the calculated default is used. Script Parameter: 3D_IDW_GRIDDING.SEARCH_RADIUS
Blanking distance	The blanking distance controls how far the voxel is extrapolated away from the nearest data point. All values at distances greater than the blanking distance are set to dummy. It only makes sense to define a blanking distance less than the search radius, since any voxel cell location farther than the search radius from the nearest data point is by definition not valued. If no blanking distance is defined, then during calculation it is set to be 4 times the horizontal cell size. Script Parameter: 3D_IDW_GRIDDING.BLANKING_DISTANCE
Cells to extend beyond data	By default, or If set to zero, the voxel extent is limited to just overlapping the most extreme data value locations in X, Y and Z. Set this to a number greater than zero to allow the voxel to be extrapolated beyond the data edges. The actual extrapolation distance is determined by the search radius, and limited by the blanking distance, and cells extended beyond this distance will remain dummies in the output voxel. Script Parameter: 3D_IDW_GRIDDING.CELLS_TO_EXTEND (Default: 0)
Log option	Select to grid your data in "log" or "log-linear" space and save the data in the transformed state or as raw data (linear). By default, the data is gridded "as is". For log gridding, the log (base 10) of the data value is used and any values less than the supplied log minimum are replaced by the log minimum. For log-linear gridding, values are first transformed as follows: Z < -log_minimum: Z - log10( -z / log_minimum ) -log_minimium <= Z <= log_minimum: Z Z > log_minimum : Z + log10( z ./ log_minimum ) This has the effect of treating large positive or negative values like logarithms, but gives a linear transform for values around zero. Script Parameter: 3D_IDW_GRIDDING.LOG_OPTION linear: 0 log, save as linear: -1 log-linear, save as linear: -2 log, save as log: 1 log-linear, save as log: 2
Log minimum	Specify the log minimum. Script Parameter: 3D_IDW_GRIDDING.LOG_MINIMUM (Default: 1)

Application Notes

*The GX tool will search in the "...\Geosoft\Desktop Applications \gx" folder. The GX.Net tools, however, are embedded in the geogxnet.dll located in the "...\Geosoft\Desktop Applications \bin" folder. If running this GX interactively, bypassing the menu, first change the folder to point to the "bin" folder, then supply the GX.Net tool in the specified format.

Anti-aliasing

Prior to gridding (and after any log or log-linear transformation), data is pre-processed using an anti-aliasing technique. All values falling inside any single grid cell are averaged, and the data is then represented by the single averaged value at the grid cell center. Any error in the spatial representation of features introduced by this step will never exceed one-quarter of the Nyquist wavelength, which is equal to 2 cell sizes.

Definition of the Weighting Slope and Power

The inverse distance weighting is a deterministic method for multivariate interpolation using a known set of data values at known locations. The grid values at each x,y point are calculated using a weighted average of the known data values within the defined search radius. The weight attributed to each known data value is inversely proportional to its distance from the grid x,y point. Applying a power to the weights will modulate the influence of each known data value as a function of distance. Furthermore adding a slope factor moderates the sharpness of the weights and prevents them from reaching a large dynamic range in close proximity to the x,y point. The weight of each of the n points within the search radius centered on a point x,y, is defined by the equation:

These weights must be normalized. The normalized weight equation becomes:

Where:

d_i  is the distance of each of the n known data values g_i within the search radius from the grid point x,y

n is the total number of g_i values within the search radius

p is a constant power

 s is a constant slope

At each grid cell x,y, the value will be calculated as:

Where:

G_xy is the output grid value at location x,y

g_i is the input data values within the search radius

Figure 1: The normalized weights (legend) of all g_i data points (indicated within the search radius) are calculated. Points outside the search radius are ignored. Then, equation G_xy=∑ⁿ_i=1W_i g_i is applied.

Using a default power of 2 and a slope of 1, produces a standard Gaussian bell-shaped weighting function. A slope > 0 ensures that the weight remains finite at zero distance. Decreasing the slope tends to flatten the bell, resulting in greater weighting of points away from the grid cell, and hence greater smoothing.

A power < 2, or a slope <1, may result in over-smoothing the data.

The following table shows the effect of various slopes on the weighting given at various distances away from the centre cell. The weights have been normalized so the weight at the cell centre is equal to 1.

	weighting of centre cell	weighting 1 cell away	weighting 2 cells away	weighting 3 cells away	weighting 4 cells away
P = 2, S = 0.2	1	0.83	0.55	0.36	0.24
P = 2, S = 0.5	1	0.67	0.33	0.18	0.11
P = 2, S = 1	1	0.5	0.2	0.1	0.056
P = 2, S = 2	1	0.33	0.11	0.053	0.03

Clearly, as the slope increases, the weighting is more tightly concentrated about the centre cell. The search radius should also be chosen based on the fall-off of the weighting function. Increasing the search radius beyond where the weighting function is significant, will have little effect on the results, and may result in large increases in processing time, since the processing time varies in proportion to the cube of the search radius. (Remember that the search radius is specified in ground units, not as a multiple of cell sizes.)

The yellow asterisk icon () displayed in front of a parameter name indicates that this parameter is required.