Derivative in the X, Y, Z Direction (DRVXYZ)
Use the Derivative option to apply a derivative filter in the X, Y, or Z direction.
Derivative Filter dialog options
|
Direction |
The direction of the derivative. The default is Z. |
|
Order of differentiation |
Order n of derivation. The default is to apply a 1st order derivative. See the Application Notes below for a mathematical exemplification of the vertical derivative. |
Application Notes
| Derivation direction | Filter operator |
|---|---|
|
X |
L(u) = (i μ) n |
|
Y |
L(v) = (i v) n |
|
Z |
L(r) = r n |
The filter operator in wavenumber domain is a function of the wavenumber domain variables μ and ν. Mathematically, the Wavenumber (Fourier) transform F(μ,v) of a 2D space domain function f(x,y) is defined as:
[1]
Where:
- x, y are the space domain variables
- μ, v are the wavenumber domain variables
The x derivative of (1) is:


[2]
Comparing (1) & (2):
- The X derivative is: - iμ F(μ,v ) (2a)
- By analogy, the Y derivative is: - iν F(μ,v ) [3]
For potential field data, Laplace’s equation states that the second vertical derivative of the field is 0: ∇^2 φ=0
That is:

[4]
This can be transformed to the Wavenumber domain by taking the derivative of the derivatives X(2) & Y(3) again and express it as:

[5]
Referring back to (4):
- The filter for the Z second derivative will then be:
- The 1st vertical derivative – the Z derivative, will be:
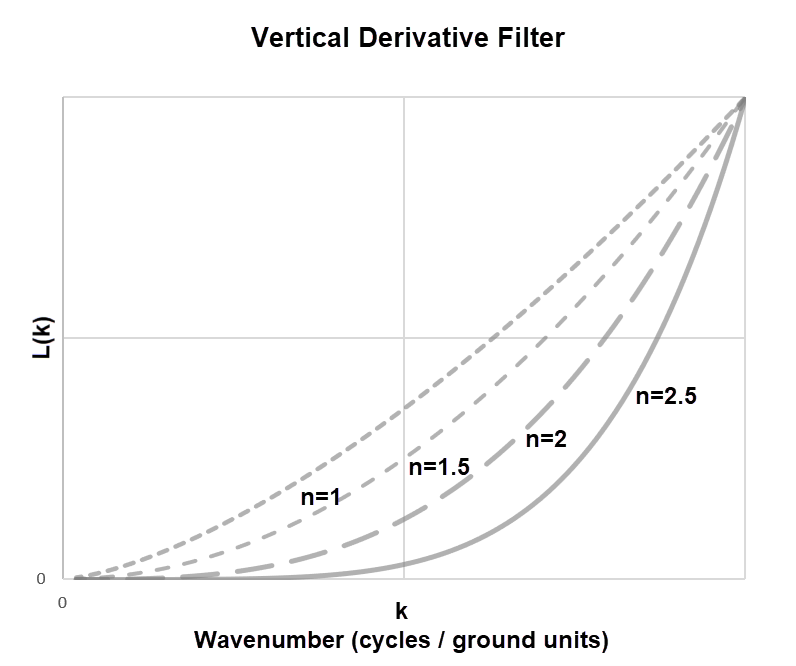
The horizontal derivative filter operators present a similar curve to the vertical derivative, but they are out of phase relative to the amplitude of the transform grid.
The horizontal derivative can be used for creating shaded images and is required for some modelling algorithms, such as Euler deconvolution.
Wavenumber domain variable definition
|
k |
Wavenumber domain increment, used to depict a radially symmetrical variable. |
where: np is the number of points cs is the cell size |
|
u |
X component in the wavenumber domain. | k = 2π ( i μ+j ν ) |
|
v |
Y component in the wavenumber domain. |
|
|
r |
Radial component in the wavenumber domain. |
|
|
θ |
Polar component in the wavenumber domain. |
|
Got a question? Visit the Seequent forums or Seequent support
© 2024 Seequent, The Bentley Subsurface Company
Privacy | Terms of Use
