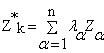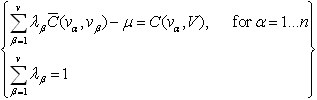Kriging Theory

Kriging is a statistical local estimation technique that provides the best linear unbiased estimate of an unknown characteristic being studied.
Oasis montaj supports ordinary Kriging as well as universal Kriging. Universal kriging differs from ordinary kriging in that it enables the data to contain a regional trend. For a more in-depth understanding of the geostatistical analysis and kriging refer to Journel and Huijbregts [1].

Ordinary Kriging

Let {Z(x) } be under study, with the following:

expectation, {Z(x) }=m ,

a constant m which is generally unknown;

centered covariance, {Z(x+h) -Z}= C (h) ;

(1)

variogram, { [Z(x+h) -Z(x) ]2} = 2g(h) ;

(2)

The experimental data to be used consist of a set of discrete values:

$image\img00013.jpg$

The linear estimate Z*k considered is a linear combination of the n data values as follows:

$image\img00014.jpg$

(3)

The weights are calculated to ensure that the estimate is unbiased, and that the estimation variance is minimal (the estimate is then said to be optimal). This calculation provides a system of (n+1) linear equations in (n+1) unknowns (the n weights and the Lagrange parameter m). This is called the kriging system.

$image\img00015.jpg$

(4)

The minimum estimation variance, or kriging variance, can be written as

$image\img00016.jpg$

(5)

Kriging system (4) can be expressed in matrix form as

$image\img00017.jpg$

where

$image\img00018.jpg$

(6)

where $image\img00019.jpg$ is the covariance between samples i and j

K is the covariance between the i'th known location and the estimation location;

w is the solution vector, which includes kriging weights and the Lagrangian.

We may note that the kriging matrix K is symmetric, i.e. $image\img00020.jpg$

Universal Kriging

The ordinary kriging (unbiased kriging of order 0) is for the stationary data, i.e. the expectation , $image\img00021.jpg$ , where m is a constant.

In practice, it may be known that a drift (non-stationary expectation) exists, i.e. a background trend of the data is not flat. In such case, we may use universal kriging (UK) (unbiased kriging of order k).

To effect UK, the kriging system (6) is expanded to include functions of position coordinates, the kriging matrix K and the vectors w and d are written:

$image\img00022.jpg$

(7)

The kriging system (7) is shown explicitly for UK in which linear drift is modeled; higher order drift models are not supported in KRIGRID.

This kriging system can also be expressed in terms of the semi-variogram function $image\img00023.jpg$ , since

$image\img00024.jpg$

where the constant Sill is any positive value greater than the greatest mean value $image\img00025.jpg$ variogram used in the kriging system.

(8)

References:

[1] C. A.G. Journel and Ch.J. Huijbregts, Mining Geostatistics (London: Academic Press, 1978).